-
프랙탈
[ fractal ]프랙탈이란 작은 구조가 전체 구조와 비슷한 형태로 끝없이 되풀이 되는 구조를 말한다.
즉, 프랙탈은 부분과 전체가 똑같은 모양을 하고 있다는 "자기 유사성" 개념을 기하학적으로 푼 것으로, 프랙탈은 단순한 구조가 끊임없이 반복되면서 복잡하고 묘한 전체 구조를 만드는 것이다.
프랙탈의 속성은 '자기 유사성(Self-Similarity)'과 '순환성(Recursiveness)'이라는 특징을 가지고 있다. 자연계의 리아스식 해안선, 동물혈관 분포형태, 나뭇가지 모양, 창문에 성에가 자라는 모습, 산맥의 모습도 다 프랙탈이며 우주의 모든 것이 결국은 프랙탈구조로 되어있다.
프랙탈이라는 말은 IBM의 Thomas J. Watson 연구센터에 근무했던 프랑스 수학자 만델브로트(Benoit B. mandelbrot) 박사가 1975년 '쪼개다'라는 뜻을 가진 그리스어 '프랙투스(fractus)'에서 따와 처음 만들었다.
만델브로트 박사는 <the nature of geometry fractal>를 출판해 냈는데, 이 책에는 "영국의 해안선 길이가 얼마일까"라는 물음을 던지고 있다. 리아스식 해안선에는 움푹 들어간 해안선안에 굴곡진 해안선이 계속됐고, 자의 눈금 크기에 따라 전체 해안선의 길이가 달라졌기 결과적으로 아주 작은 자를 이용하면 해안선의 길이는 무한대로 늘어나게 되는 것이다. 그는 이처럼 같은 모양이 반복되는 구조를 ‘프랙탈’이라고 부르기 시작했다.- 출처 : 시사용어사전, 2005
프랙탈
[ fractal ]1차원, 2차원 등의 정수 이외의 차원을 갖는 도형. fraction이란 단어가 분수나 단수를 의미하기 때문에 구름의 형태나 숲의 수관 등 자연물의 형상을 수학적 대상으로 파악하고 표현하기 위해 도입하였다. 프랙탈은 자기상사성, 즉그 어느 부분을 확대해 보더라도 전체와 같은 도형이 나타나는성질을 갖고 있다. 예를 들면 리아스식 해안의 해안선과 같은자연계 물체의 형태가 프랙탈로 근사한다고 생각하는 것이다.수학적으로는 100년 전 쯤에 Koch곡선, 페아노곡선 등의 프랙탈도형을 연구하였다.
- 슈뢰딩거의 고양이
자연의 찌그러진 기하학
세계의 기하학은 우리가 상상하기 쉽고 계산하기 편하도록 평면이나 직선으로 이루어져 있지 않다. 자연은 온통 갈라지고 모나고 울퉁불퉁한 대상으로 가득 차 있다. 해안선은 예리하게 각져 있고, 나무껍질은 조각조각 갈라져 있고, 숲은 들쑥날쑥하고, 강물은 구불구불 휘어져 있고, 지표는 울퉁불퉁하고, 아스파라거스 줄기의 끝은 꺼칠하며 길고, 브로콜리는 우둘투둘하다. 자연에는 모든 형태가 다 가능하지만 우리 인간이 만든 연필이나 자, 액자 따위에서 볼 수 있는 매끄럽고 반질반질한 모습은 없다. 세계의 기하학은 유클리드가 보여주려고 했던 것처럼 반듯하지 않다.
1970년대에 만델브로트는 아주 특별한 단어를 학계에 소개한다. 지금은 일반적으로 널리 사용되면서 우리의 문화를 더욱 풍요롭게 만들어주는 이 단어가 바로 '프랙탈(fractal)'이다. 프랙탈은 '부수다'는 뜻의 라틴어 '프랑게레(frangere)'에서 나온 말로서 '단편(fragment)'이나 '파편(fraction)' 등을 가리키는 일상언어에서도 그 흔적을 찾아볼 수 있다. 프랙탈은 그러니까 반듯한 가장자리가 없는 물체를 뜻하는 단어다.
가장 유명한 최초의 프랙탈은 앞에서 소개한 만델브로트 세트다. 경계선이 반듯하지 않은 물체를 프랙탈이라고 말할 때 이 말의 의미에는 직선뿐만 아니라 곡선도 포함된다. 물론 곡선은 이리저리 휘어 있지만 그중 한 부분을 잘라내어 무한히 확대시키면 결국에는 직선이 된다. 그런데 프랙탈은 이런 형태의 선으로 이루어진 도형이 아니다. 만델브로트 세트에서 임의로 한 부분을 잘라내어 그 선을 확대시켜보면 계속해서 굴절이 나타나는 것을 발견할 수 있다. 아무리 크게 확대시켜도 앞의 경우와 같은 곧은 선은 나타나지 않는다. 즉 프랙탈은 경계선이 절대로 직선이 될 수 없는 물체이다.- 출처 : 슈뢰딩거의 고양이, 에른스트 페터 피셔, 2009.1.20, 들녘
신비한 "프랙탈"
세 가지 그림을 살펴볼까요?
<그림 1>은 눈의 결정과 같은 모양입니다.
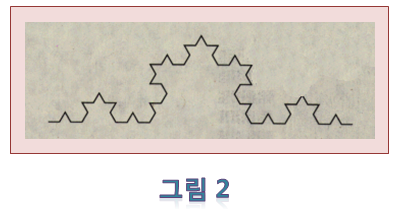
<그림 2>는 처음 그림을 셋으로 나눈 그림입니다. 즉 이 그림을 세 번 연결하면 처음 그림이 나옵니다.
<그림 2>를 다시 네 부분으로 나누어 보면 <그림 3>이 됩니다.
네모 안의 모양을 잘 살펴보면, <그림 1>의 모양와 같습니다.
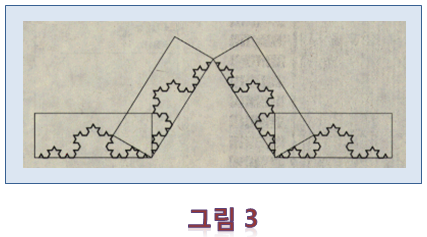
이와 같이 자기 자신과 닮은 도형을 반복하여 얻을 수 있는 그림을 "프랙탈"이라고 합니다.
즉 프랙탈이란 작은 구조가 전체 구조와 비슷한 형태로 끝없이 되풀이되는 구조를 말합니다. 쉽게 자기닮음 도형이라고 이해하시면 좋을 것 같습니다. 커다란 구조를 작게 봐도 똑같은 구조를 가지는 형태이지요.
생활에서 프랙탈을 찾아보면 구름, 나뭇가지, 사람의 혈관, 산의 모양 등등 자연에서 관측되는 것들은 거의 프랙탈의 형태를 띠고 있다고 합니다.
프랙탈이라는 말은 IBM의 Thomas J. Watson 연구센터에 근무했던 프랑스 수학자 만델브로트(Benoit B. mandelbrot) 박사가 1975년 '쪼개다'라는 뜻을 가진 그리스어 '프랙투스(fractus)'에서 따와 처음 만들었다고 합니다.
[스토리텔링 수학 속으로] 폐, 부피에 비해 면적 넓은 이유… 색종이 안쪽 잘라 비교하면 아하!<2> 프랙탈 도형과 몸물고기의 아가미, 사람의 혈관, 폐와 장의 내부의 공통점은 부피에 비해 표면적이 넓은 것이다. 잔주름, 모세혈관, 허파꽈리 등을 가진 구조여서 그렇다. 사람 피부의 총 표면적은 약 2㎡이다. 반면 폐의 표면적은 약 80㎡이고, 소화관의 표면적은 무려 약 400㎡라고 한다. 또 사람 혈관의 길이는 약 10만㎞에 이른다고 한다. 이같이 주어진 부피에 비해 엄청난 길이나 면적을 가지는 것을 수학적으로 설명할 수 있는 방법이 바로 프랙탈의 원리다.
앞에 예를 든 몸의 일부는 작은 구조가 전체 구조와 비슷한 형태로 끝없이 되풀이되는데 이러한 구조가 프랙탈이다. 프랙탈의 예는 창문에 성에가 자라는 모습, 반복되는 산맥의 모습, 동물의 순환계·소화관·신경계, 나뭇가지의 모양, 리아스식 해안선 등 일상 생활에서 쉽게 발견된다.
이 원리가 수학에 적용된 것이 '프랙탈 도형'이다. <그림1>을 보자. 각 프랙탈 도형을 단계적으로 무한 반복하면 코흐눈송이는 넓이가 늘어나고, 시어핀스키삼각형은 넓이가 0에 가까워진다. 하지만 둘 다 도형의 둘레는 무한대로 늘어난다. 시어핀스키피라미드는 단계를 반복하면 부피는 0에 가까워지고 겉넓이는 처음 모양(0단계)과 같게 유지된다. 반면 밍거스폰지는 부피는 0에 가까워지지만 겉넓이는 무한히 늘어난다. 밍거스폰지와 같은 프랙탈의 원리가 제한된 부피 안에 넓은 표면적을 확보해야 하는 신체 기관에 적용돼 있는 것이다.
이제 초등학교 4학년 문제를 통해 프랙탈 도형에 대해 알아 보기로 하자. <그림2>는 가위로 자른 4장의 색종이다. 각각의 둘레를 직관적으로 비교해 "①, ③의 둘레는 같고 ②, ④는 이보다 길다"고 대답한다면 프랙탈 도형을 제대로 이해했다고 할 수 있다. ②처럼 네모난 색종이에 오목한 곳이 생기게 자르거나, ④처럼 색종이 내부를 잘라내면 넓이는 작아지지만 둘레는 늘어난다. 안쪽으로 파고드는 부분이 없는 ③은 넓이는 줄지만 둘레는 ①과 같다.
사람의 폐가 부피에 비해 면적이 매우 넓은 이유를 설명할 때 프랙탈이라는 말을 몰라도 색종이의 안쪽을 잘라내 넓이는 줄지만 둘레가 늘어나는 것과 비교해 설명할 수 있어야 한다. 이같이 스토리텔링 수학은 개념의 암기가 아니라 개념의 응용에 더 무게를 둔다.출처 : 한국일보
