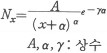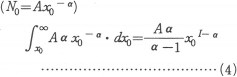파레토의 법칙(Pareto's law)

두산백과

파레토의 법칙

[ Pareto's law , ─法則 ]

로잔학파에 속하는 이탈리아의 경제학자 V.파레토에 의해 발표된 소득분포의 불평등도(不平等度)에 관한 법칙.

소득분포에 관한 실증분석면에서의 독창적인 업적을 담은 저서 《경제학강의：Le Cours d’économie politique》(2권, 1896∼1897)를 통해 발표한 내용에 의하면, 소득이 y 이상인 인원수 N(y)와 y와의 사이에는 log N(y)＝B－α log y 의 경험적 법칙이 존재한다. 이 경우 α(파레토 定數)의 수치가 클수록 소득의 불평등도는 높다. 그 후의 연구에서는 파레토의 법칙이 성립하는 것은 중 정도의 소득보다 높은 사람들에게 한정된다는 사실이 밝혀졌다.

따라서 이 법칙을 이용하여 α를 계측하는 데는 먼저 양대수(兩對數) 그래프에 y와 N을 기입한 다음 양자의 관계가 직선에 가까워지는 범위에 대해 최소자승법을 적용하면 된다. 이 법칙은 부의 분포 비교 등에도 사용된다. 소득분포의 불평등도를 계측하는 방법으로는 파레토의 법칙 이용 외에 로렌츠곡선에 의한 비교, 지브라의 법칙을 사용하는 방식 등이 있다.

참조항목

ABC분석, 최소제곱법, 빌프레도 파레토

역참조항목

계약곡선, 분배, 지니의 법칙, 지브라의 법칙, 개인적 분배, 과두제에 대한 현대 정치 이론, 롱테일법칙

출처 : 두산백과  

------------------------------------------------------------------------------------------------------------

경제학사전

파레토 법칙

[ ~法則 , Pareto's law ]

파레토 법칙은 소득분포에 관한 통계적 법칙으로서, 파레토가 유럽제국의 조사에서 얻은 경험적 법칙이다. 이제 x를 소득액, N_x를 x이상의 소득을 지닌 사람의 수(고액자부터 누계)로 하고, A, α, r를 통계적으로 정해진 상수라고 하면

즉, logN_x=logA-αlog(x+α)-rα라는 법칙이 성립된다. 그러나 보통 근사식으로서 쓰이는 것은,

N_x=Ax^-α 또는
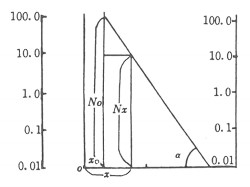
logN_x=logA-αlogx…………………(1)이다

종축에 logNx를, 횡축에 logx를 표시하여 (1)식을 그림으로 나타내면 소득자의 누적분포곡선은 대략 직선이 되고 이 선과 횡축과의 경사가 α이다. 소득계층의 x에 있어서의 소득자 수는 (1)식을 미분하여

그의 총소득액은, (2)식에 소득액 x를 곱하여

Aαx^-(α-1)x=Aαx^-α…………………(3)

로 나타난다. 따라서 최저소득 x₀ 이상의 소득의 누계는, 전소득자 수를 N₀로 하면 (N₀=Ax₀^-α)

이다. 평균소득액을 M₀으로 하면, 그것은 (4)식을 총소득자 N₀로 나누어

x 이상의 소득을 가진 사람의 수(N_n)의 전소득자수(N₀)에 대한 비율은

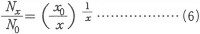이다

x 이하의 소득자의 나머지 합계를 y로 하면,

평균소득(M₀)와 x 이상의 소득의 평균액(M_x)과의 비율은

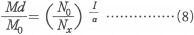이다.

파레토곡선의 기울기 α는 소득분포의 불평등도(degree of inequality)를 보이는 하나의 척도이다. 파레토는 α가 작을수록 분포가 평등하다고 하였으나, 지니 이후의 많은 연구에 의하면 α가 클수록 소득의 균등화를 보이게 된다. 그러나 이러한 차이는 불평등의 정의에서 비롯되는 바가 크다. 파레토는 소득자 수에 주목하여 'x 이하의 소득인원이 x 이상의 소득인원에 비하여 감소할 때에 소득의 불평등이 감소된다'라고 정의한다. 즉 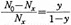가 적을수록 평등하고, 클수록 불평등하다고 말한다. 이것은 (6)식에 있어 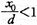이므로 α가 큰 만큼 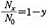가 적게 되고, 따라서 불평등이 큰 것을 뜻한다. 그러나 소득자 수가 아니고 금액에 주목하면 (8)식의 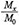가 적을수록 소득은 균등화되었다고 말할 수 있다. 또 (8)식에 있어 α가 큰 만큼 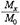는 적다.

파레토법칙이 완전한 타당성을 지니려면, 소득곡선은 직선이 되어야 한다. 그러나 저소득층에 가까울수록 곡선은 굴절하여 수평선에 가깝게 되고, 따라서 α가 불평등의 척도로 타당하느냐 하는 데 대해서는 논의의 여지가 있다. 이것은 하나는 대수 log 눈금을 사용하여 보기 때문이고 또 저소득층 수가 그것보다 높은 소득자에 비하여 퍽 적기 때문이다. 파레토 방정식에서는 소득(x)→∞일 때 인원(N)이 0가 되고, x=0일 때 N→∞가 되므로 최고와 최저의 부분에 관해서는 적확하지 못하다.

파레토 법칙

파레토는 α의 값이 대략 1.5이며, 예를 들어 1893~94년 영국은 1.50, 1894년 프러시아는 1.60, 1886년 파리는 1.57 등 모든 시대의 모든 국민에 있어 소득분포는 안정되고, 그 불평등도가 때와 장소에 관계없이 일정하다고 단언하였다. 그러나 그 후의 연구에 의하면 α의 감도가 민감하지 못하여 그것에 의한 소득분포의 일정성을 말하는 것은 매우 위험하다는 결론에 이르고 있다.

참고문헌

• Pareto, V., Cours d’économie politique, 2 Vols., 1896~97
• Manuel d'économie politique, 1909

참조어

지니의 법칙

출처

경제학사전, 2011.3.9

세계화라는 거센 도전 속에 모든 경제분야의 급속한 변화를 겪고 있다. 이에 따라 새로운 경제이론과 경제용어가 쏟아져 나오고 있다. 이런 이유로 최근에는 신문과 잡지등에서 경제...자세히보기

편저 박은태

제공처 : 경연사 http://www.genyunsa.com/new/genyunsa/genyunsa.htm, 제공처의 다른 책보기