황금분할

황금분할

[ golden section , 黃金分割 ]

선분을 한 점에 의하여 2개의 부분으로 나누어, 그 한쪽의 제곱을, 나머지와 전체와의 곱과 같아지게 하는 일을 말한다.

작도의 예

하나의 선분 AB가 있을 때, 그 선분상에 한 점 P를 구하여

(AP)²=BP·AB

가 되도록 하는 일이다.

BP:AP＝2:(√5 + 1)＝1:1.61803…

을 황금비(黃金比) 또는 외중비(外中比)라 한다. 또, 정오각형의 같은 꼭지점[頂點]을 지나지 않는 두 개의 대각선(對角線)은 서로 다른 쪽 대각선을 황금분할한다. 황금비를 분수로 근사 표현을 하면 다음과 같다.



황금비는 고대 그리스에서 발견되었고, 가장 조화가 잡힌 비(比)로서 이와 같이 이름하게 된 것인데, 르네상스의 볼로냐의 수도승(修道僧) 루카 파치올리(Luca Pacioli)에 의하여 ‘신성비례(神聖比例)’라고 이름할 정도로 중요시되었다.

특히 시각(視覺)에 호소하는 도형이나 입체 등에서는 이 비를 많이 이용해왔으며, 예를 들면 직사각형의 두 변의 비가 황금분할이 되는 것은 여러 가지 비례의 직사각형 중에서 가장 정돈된 직사각형이라 하였다. 건축·조각·회화·공예(工藝) 등, 조형예술의 분야에서는 다양한 통일의 하나의 원리로서 널리 활용되고 있다.

또, 자연의 조화가 잡힌 형태 중, 예를 들면 잎맥[葉脈], 종자의 형상, 조개껍데기 소용돌이, 세포의 성장 등에서 이 비를 찾아내려고 하는 사람도 있다. 근년에는 음악 영역에서도 이것을 작곡에 활용한 예가 있다. 황금비는 일상 생활 속에서 쉽게 찾을 수 있다. 예를 들면 엽서, 담배갑이나 명함의 치수 등도 두 변의 비가 황금비에 가깝다. 물건을 선택할 때 대부분의 사람은 무의식 중에 황금비의 치수를 취하고 있다.

참조항목

비례, 피보나치수열

역참조항목

외중비

출처

두산백과

[출처] 황금분할 | 두산백과

1.황금비(黃金比) 또는 황금분할(黃金分割)

황금비 또는 황금분할은 주어진 길이를 가장 이상적으로 둘로 나누는 비로 근사값이 약 1.618인 무리수입니다. 기하학적으로 황금분할은 이미 유클리드(원론 3, 141)가 정의한 이래 예술분야, 특히 건축, 미술 등에서 즐겨 응용되고 있습니다.

인간은 황금비를 보면 무의식적으로 아름답다고 느낀다고 합니다. 건축물의 기하학적인 아름다움, 고대의 유명한 그림, 꽃이나 생물체에서의 신비, 8등신 미인 등은 동서양을 막론하고 누구나 느끼는 아름다움의 대상이 되는데 바로 황금분할로 구성이 되어 있기 때문입니다. 우리 생활에서 가까이 볼 수 있는 것은 명함, 담배갑, 신용카드 등의 가로, 세로 비율이 바로 황금비에 해당합니다.

황금비에 대한 좀 더 자세한 설명을 드리면,

“전체에 대한 큰 것의 비가 큰 것에 대한 작은 것의 비와 같다. (단, 전체는 큰 것 + 작은 것)” 입니다.

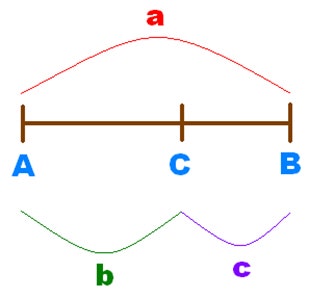
전체 선분 AB를 a로, 큰 것 AC를 b로, 작은 것 CB를 c로 보겠습니다.

황금비의 정의로 보면 a : b = b : c 가 되겠지요? 잠시 학창시절로 돌아가서 간단한 수학으로 계산을 해봅시다. 너무 긴장하지 마시구요. ^^

a : b = b : c

b² = ac

그런데 c는 a - b라고 할 수 있겠지요?

b² = a(a-b)

b² = a² - ab

a² - b² - ab = 0

우리는 비율을 알고자 하는 것이므로 a 값에 1을 치환하여 풀어 보겠습니다.

1 - b² - b = 0

b² + b - 1 = 0

어디서 많이 본 모양새 입니다. 이차 방정식의 해법인 근의 공식에 대입할 수 있겠지요? 기억을 되살리기 위해 또 설명 드립니다.

근의 공식에 대입하면

b = ( √5 - 1 ) / 2

가 됩니다.

즉 황금비는 a : b 이므로

1 : ( √5 - 1 ) / 2 는 약 1 : 0.618 .

또한 a : b = b : a - b 이므로

b : a - b 는

( √5 - 1 ) / 2 : 1 - ( √5 - 1 ) / 2 는 약 1.618 : 1 정도가 됩니다.

이해 하시겠지요? 설령 이 부분이 이해가 되지 않더라도 너무 걱정은 하지 마십시오. 그냥 그런 것이 있구나 하고 넘어 가시면 되겠습니다.

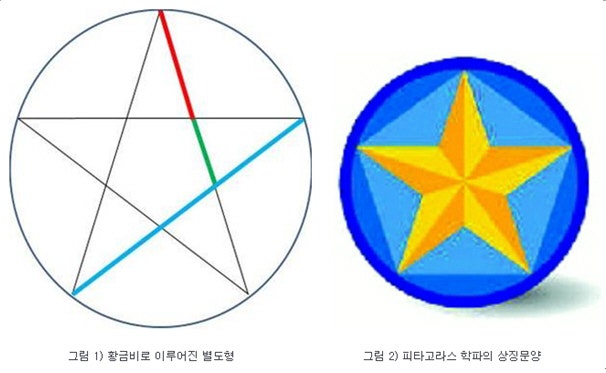
황금비를 최초로 발견한 사람을 그리스의 피타고라스로 추정하고 있는데요, 그는 모든 현상을 수로 표현하려고 노력하였는데 어느 날 정오각형 안에 별 모양을 이루는 모든 선분이 황금비로 되어 있기 때문이었습니다. 그는 인간이 생각하는 가장 아름다운 비를 황금비라 여겨 황금 분할의 비율이 내재된 정오각형 모양의 별을 피타고라스학파의 상징으로 삼았다고도 합니다.

2.피보나치 수열 (Fibonacci Sequence)

피보나치 수열은 첫 번째 항의 값이 0이고 두 번째 항의 값이 1일 때, 이후의 항들은 이전 두 항을 더한 값으로 이루어지는 수열을 말합니다.

이를 테면, 제3항은 제1항과 제2항의 합, 제4항은 제2항과 제3항의 합이 되는 것과 같이, 인접한 두 수의 합이 그 다음 수가 되는 수열인 것입니다. 즉, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,… 인 수열이며, 보통 a1＝a2＝1, an＋an+1＝an+2 (n＝1,2,3…) 로 나타냅니다. 이것은 L.피보나치가 1202년 《산술(算術)의 서(書)》에서 처음으로 제기하였는데요, 이렇게 단순한 수열이 중요해진 것은 이 수열이 자연계의 일반 법칙을 나타내는 것으로 보이기 때문입니다.

피보나치 수열의 인접한 두수의 비(뒷수와 앞수의 비)를 분수의 형태로 하여 수열을 만들면,

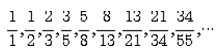
또는

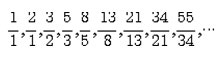
와 같이 되는데, 이 두 수열은 각각

(√5－1)/2＝0.6180339…와

(√5＋1)/2＝1.6180339…

에 수렴합니다.

이것 어디서 본 것이죠? 네~ 바로 앞서 살펴 보았던 황금분할의 비이지요?

뭔가 흥미롭지 않습니까?

잠시 머리를 식히고 다음 장으로 넘어가 봅시다. ^^

3.피보나치수열의 응용

지수가 오르고 내리는 현상을 파동이라 할 수 있는데 이 파동은 매수자와 매도자의 힘의 크기와 시세주도세력에 의해 궤적을 그려 나갑니다.

지수는 첫 거래 가격이 시가로, 가장 낮은 거래 가격이 저가로, 가장 높은 거래 가격이 고가로 명칭이 됩니다. 그러나 이렇게 단순하게 결정이 나는 듯한 주가의 결정 원리이지만, 우리는 일명 세력이라고 불리는 무형의(?) 존재들로부터 각종 외부적인 요소들에 의해 철저하게 인위적으로 만들어 가는 차트의 모습을 보게 되는데, 이때 일정한 규칙이나 패턴들이 존재하게 됩니다.

엘리어트(Elliott)는

“인간의 모든 행동은 패턴과 비율과 시간이라는 세 가지 요소로 구성되어 있는데, 이는 피보나치 수열의 원리와 합치하는 것이다.”

라고 했으며, 주가의 움직임도 패턴과 비율과 시간에 의해 결정된다고 할 수 있습니다.

“주가는 일정한 규칙에 의해서 만들어져 간다.”

출처 : http://cafe.naver.com/dnainvest/130