-
출처 : http://navercast.naver.com/contents.nhn?rid=20&contents_id=2389

빅뱅우주론은 정상상태우주론과의 경쟁에서 최종적으로 승리하였지만, 우주학자들의 관심이 집중되고 얼마 안 있어 두 가지 심각한 문제에 직면하게 되었다. 그것은 우주의 평탄성 문제(flatness problem)와 지평선 문제(horizon problem)였다.
빅뱅우주론의 첫 번째 문제점 : 우주의 평탄성 문제

우주는 계속 팽창할까? 아니면 어느 시점에 다시 수축할까?
빅뱅 이후 우주는 100억 년 이상 팽창을 계속하고 있다. 우주의 미래에도 계속 팽창하게 될까? 아니면 언젠가는 팽창을 멈추고 다시 수축하게 될까? 우주가 팽창하는 동안에도 우주 안의 물질들 사이에는 서로 끌어당기는 인력(중력)이 작용하고 있다. 따라서 우주의 팽창은 일종의 브레이크가 걸려 있는 상태이므로, 언젠가 우주의 팽창이 멎게 되면 중력에 의해 우주는 다시 수축하게 될 것이다.
우주가 팽창을 계속하게 될지, 아니면 팽창을 멈추고 다시 수축하게 될지는 우주 안에 있는 물질의 양이 얼마나 되는가에 달렸다. 이 물질의 양을 표현하는 방식으로는 우주의 밀도라는 개념을 사용하는데, 특히 우주의 팽창을 멈추게 하는 특별한 우주의 밀도 값이 존재한다. 이를 임계밀도(critical density)라고 한다.
우주의 임계밀도는 여러 연구를 통해 10-29g/cm3로 알려졌다. 이 값은 1세제곱미터의 우주공간 안에 겨우 6개의 수소 원자가 있는 것에 불과하다. 이 값은 깜짝 놀랄 정도로 작은 것이다. 이 밀도는 행성 사이의 공간 밀도보다 1억 배나 높은 고진공이고, 지구상에서 얻을 수 있은 가장 높은 진공보다 훨씬 더 완전진공에 가깝다. 참고로 우리 대기 중에는 1세제곱미터 안에 1025개의 원자가 있다.
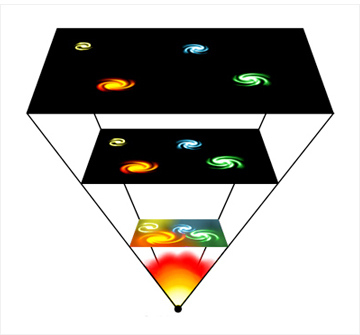
우리 우주는 언젠가 팽창을 멈추고, 다시 수축하여 대함몰(Big Crunch)로
끝날 수 있다. <출처: Bjarmason at en.wikipedia.com>우주의 운명은 Ω 값이 1보다 큰지 작은지에 따라 결정된다
그러면 우주의 평균밀도는 얼마나 될까? 우주학자들은 흔히 평균밀도 대신 Ω(오메가)라는 값을 정의하여 사용한다.

만일 Ω<1이면 우주의 밀도는 임계밀도보다 작아서 우주는 끝없이 팽창하는 열린 우주(open universe)가 된다. 이런 우주공간에서 두 평행선은 서로 만나지 않으며, 삼각형의 내각의 합은 180°보다 작은 음의 곡률을 갖는다. 반대로 Ω>1이면 중력이 충분히 커서 우주는 어느 시점에서 팽창을 멈추고 다시 수축하는 닫힌 우주(closed universe)가 된다. 이런 우주공간에서 평행선은 어딘가에서 반드시 만나며 삼각형의 내각의 합은 180°보다 큰 양의 곡률을 갖는다. 특별한 경우는 Ω=1인 경우이다. 이때 우주는 열린 우주와 닫힌 우주의 중간상태를 절묘하게 유지하면서 영원히 팽창하게 된다. 이런 우주공간에서 삼각형의 내각의 합은 180°가 되며 곡률이 없는 평탄한 우주(flat universe)가 된다.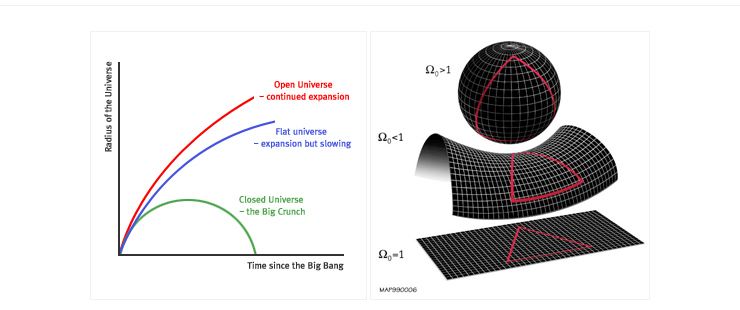
우주의 미래. 우주의 미래는 세 가지 가능한 시나리오로 설명될 수 있다. Ω<1이면 우주는 계속 팽창하다가
전체적으로 얼어붙게 되고, Ω>1이면 언젠가 팽창을 멈추고 수축되기 시작하여 대함몰(Big Crunch)로 끝난다.
그리고 Ω=1이면 우주는 평탄한 상태를 유지하면서 영원히 팽창한다.
그렇다면 우리 우주는 어떤 상태일까? 그것을 알려면 우리 우주의 Ω 값을 알아야 된다. 이 값은 암흑물질이나 암흑에너지의 포함 여부에 따라 달라진다. Ω의 값은 항성들의 질량만으로 계산해도 0.01 이상이며, Ω의 값이 1에서 크게 벗어나지 않을 것으로 예상한다. 왜냐하면 Ω의 값이 1보다 매우 크다면, 우주의 팽창은 급격하게 제동이 걸려 우주의 팽창 속도가 크게 감속된 다음, 팽창을 멈추고 다시 수축하게 된다. 



브레이크가 고장난 자동차처럼 계속 팽창만 하는 우주는 가속도가 붙어서 공간
팽창의 한계점을 넘어갈 수 있다. 이때, 우주공간이 찢어져버린다는 가설이 있고,
이를 찢어짐 이론(Big Rip)이라고 한다.반대로 1보다 매우 작다면 우주가 커짐에 따라 Ω의 값은 급격히 작아지므로, 우주는 끝없는 팽창만을 하게 된다. 수치로 예를 들자면, Ω=2일 경우 우주의 크기가 2배로 늘어나기 전에 우주는 팽창을 완전히 멈추고 수축단계로 들어가게 되며, Ω=0.5일 경우 우주의 크기가 2배로 커지면 Ω=0.25로 줄어들게 되어 우주는 계속 팽창하게 된다.
우리 우주의 Ω값은 1에서 크게 벗어나지 않는다
이러한 이유 때문에 Ω의 값이 1로부터 조금만 벗어나면 그 편차는 오랜 팽창 기간(우주의 나이: 137억년)동안 엄청나게 증폭된다. 따라서 우주가 너무 오래전에 수축하여 사라져버리지도 않았고, 너무 빨리 팽창하여 은하나 별들이 생성될 여유가 없이 커져 버려서 은하나 별이 거의 없는 우주가 되어버리지 않는 유일한 방법은 Ω가 1에 매우 근접하는 경우이다. 이 때문에 우리 우주의 Ω 값이 1에서 크게 벗어나지 않을 것으로 추측하는 이유이다.
평탄성의 문제 : Ω 값이 1과 거의 같다는 것이 과연 우연일까?
빅뱅 순간, Ω는 어떤 값을 갖고 있었을까? 현재 우주의 밀도는 임계밀도에서 크게 벗어나지 않았고, 우주는 137억 년 동안 팽창을 계속해왔기 때문에 과거의 우주는 현재보다 임계밀도에 더욱 가까이 접근했을 것이고, 빅뱅의 순간에 다가갈수록 그 정도는 더욱 심해질 것을 예상할 수 있다. 오늘날 Ω의 값이 0.1~10 범위의 값을 갖는다고 가정하면, 빅뱅 후 1초가 지났을 때 Ω의 값은 1의 값에서 10-15 정도의 차이를 가졌을 것이다. 즉 Ω=1.000000000000000이어야 한다. 그리고 물리학적으로 상상할 수 있는 가장 짧은 순간(플랑크 시간 : 10-43초), 즉 우주 탄생의 순간에 Ω는 1.0000000000 0000000000 0000000000 0000000000 0000000000 0000000000이어야 한다는 것을 의미한다.
이것은 우주가 팽창을 시작할 때 팽창과 중력이 믿을 수 없을 정도로 정확하게 조정된 상태에서 출발했으며, 우리 우주가 곡률이 없는 평탄한 우주라는 것을 말해준다. 이것을 미세조율의 문제(fine tuning problem) 또는 평탄성의 문제라고 부른다.
빅뱅우주론의 두 번째 문제점 : 우주의 지평선 문제

우주의 크기는 기준에 따라 다르지만, 상상 이상으로 거대하다
우주는 유한한가 아니면 무한한가? 사실 우리는 그것을 알지 못한다. 그래서 천문학자들은 가시적 우주(visible universe)라는 개념을 사용한다. 가시적 우주는 우주가 팽창을 시작한 이래 빛이 우리에게 도착할 때까지 진행해온 영역으로 정의한다. 따라서 가시적 우주는 중심에 우리가 있고 반지름이 137억 광년 되는 가상적인 구로 생각할 수 있다.
또 다른 우주의 개념으로 관측 가능한 우주(observable universe)가 있다. 가시적 우주에서 우리가 볼 수 있는 우주의 지평선은 137억 광년 거리에 있지만, 우주는 팽창을 계속하고 있기 때문에 현재 이 지평선은 그보다 훨씬 더 멀리 가 있다. 우주의 팽창을 고려할 때 우주의 반경은 465억 광년이 된다. 우주가 팽창하고 있으므로 가시적 우주나 관측 가능한 우주는 모두 시간이 갈수록 커진다.

가시적 우주. 허블 우주망원경으로 관측한 가장 먼 우주 사진(HUDF)
거의 우주의 지평선까지 관측한 사진이다. <출처: NASA>관측을 해본 우주는 거대한 규모에서 볼 때, 균일하다
빅뱅 우주 모형에서 제기된 또 다른 문제는 우주의 지평선 문제이다. 이 문제는 우주 은하들의 분포가 전체적으로 매우 균일하다는 사실로부터 기인한다. 우주 공간의 은하들은 은하단과 초은하단이라는 구조를 이루며 분포하지만, 이보다 더 큰 거대규모에서 볼 때 전 우주의 물질 분포는 균일하다. 또 우주배경복사 역시 우주의 물질이 전 우주에 걸쳐 매우 고르게 분포하고 있음을 말해준다. 우주배경복사탐사선(COBE)을 통하여 관측된 우주배경복사는 빅뱅으로부터 38만 년 후의 우주의 밀도분포를 보여주는데, 전 우주에 걸쳐 1/10만 범위의 오차 내에서 고르게 분포하고 있음을 보여준다. 이와 같은 사실들은 우주가 전체적으로 고르게 분포하고 있을 뿐 아니라 모든 방향으로 대칭적으로 팽창하고 있음을 말해준다.
이것은 매우 납득하기 어려운 사실이다. 가시적 우주의 끝에서 끝까지의 거리는 137억 광년×2 = 274억 광년이다. 이 거리는 우주의 나이(137억 년) 동안 빛이 도달할 수 없는 거리이다. 우주가 균일해지기 위해서는 우주의 모든 곳, 우주의 한쪽 끝과 그 반대쪽 끝이 서로 정보를 교환할 수 있어야 한다. 하지만 이들은 빛의 속도로도 도달할 수 없을 만큼 멀리 떨어져 있다. 그럼에도 불구하고 우주의 모습이 어디나 똑같이 닮아있는 것이다.
오늘날 지구촌 사람의 패션은 시간 차이 없이 전 세계가 거의 동조화되어 가고 있다. 같은 패션이 여러 나라에서 거의 동시에 유행하고 있다. 이런 일이 가능해진 것은 전 세계가 매스컴과 네트워크로 서로 연결되어 있기 때문이다. 하지만 이런 일은 고대나 중세에는 전혀 가능하지 않았다. 나라마다 개성 있는 고유의 의상을 입고 있었다. 당시에는 정보전달이 동시대적으로 이루어지기 않았기 때문이다. 이로부터 알 수 있는 것은 자연은 서로 단절되어 있을 때 균일성보다는 다양성이나 독창성이 나타난다는 것이다.
지평선 문제 : 우주는 상호 정보 교환이 불가능 할 정도로 큰데, 균일할 수 있을까?
하지만 우리 우주는 서로 아무런 정보를 주고받을 수 없을 만큼 멀리 떨어져 있음에도 어디나 똑같이 닮아있다. 우주는 균일하고 우주의 모든 부분이 똑같은 물리법칙을 따르면서 똑같은 방식으로 동시에 팽창하고 있다. 이것을 우주의 지평선 문제라고 한다. 이러한 문제가 제기되는 것은 중력이 우주의 팽창을 늦추기 때문이다. 우리 우주가 현재보다 더 젊고 더 압축되어 있었을 때, 우주는 더 빨리 팽창하고 있었고 서로 간에 신호 전달이나 어떤 인과적인 접촉이 일어날 수 있는 시간도 훨씬 적었다.
인플레이션 이론의 등장 : 우주가 초기에는 빛 보다 빠르게 커졌다


우주의 인플레이션을 제안한 앨런구스
<출처: Betsyhedevine at en.wikipedia.com>우주학자들이 빅뱅우주론에서 불거진 이와 같은 문제 때문에 골머리를 앓고 있을 때, 스탠퍼드 선형가속기 센터에서 일하고 있던 앨런 구스는 1979년 12월 어느 날 우주가 태어나자마자 엄청나게 빠른 속도로 팽창했다고 가정하면 이런 수수께끼들을 모두 해결할 수 있다는 사실을 발견했다. 구스는 입자물리학 이론의 하나인 대통일장이론(GUTs)에서 제기된 자기홀극 문제를 해결하기 위해 이 가설을 제안했지만, 곧 빅뱅우주론의 문제들을 해결할 수 있음을 알았다.
인플레이션이라 불리는 이 이론은 우주 초기의 어떤 순간에 우주가 빛보다 더 빠른 속도로 팽창했다는 가설이다. 이것은 빅뱅 속에서 극미한 순간 동안 기하급수적으로 우주의 팽창이 일어나 우주의 크기가 엄청나게 커졌다는 것이다.
아인슈타인의 특수상대성이론에 의하면 모든 물체는 빛보다 빨리 운동할 수 없다고 생각할지도 모르지만 꼭 그렇지만은 않다. 특수상대성 이론은 공간 안에서 운동하는 물체에 적용되는 것이지 공간 자체의 팽창에는 적용되는 것이 아니기 때문이다.
다른 학자들도 이와 비슷한 결론에 도달했다. 대통일장이론에서 주장하는 힘의 상전이가 일어날 때 10-35초마다 2배씩 증가하는 극단적인 가속팽창이 일어날 수 있다는 것이다. 인플레이션이 일어난 시기는 대폭발 후 10-37초에서 10-33초까지로, 이 짧은 시간 동안 시공간은 빛 보다 빠른 속도로 팽창하여 우주의 크기는 양성자보다 훨씬 작은 크기에서 1026배 이상 커졌다는 것이다.
인플레이션이론으로 평탄성과 지평선 문제를 설명할 수 있다

인플레이션이론을 도입하면 우주의 지평선 문제는 쉽게 설명할 수 있다. 인플레이션에 의해 우주의 크기가 빛의 속도보다 더 빠르게 팽창하므로 인플레이션이 일어날 당시의 우주의 지평선 거리는 현재 빛이 도달할 수 없는 거리보다 훨씬 바깥으로 밀려나가 버린다. 따라서 현재 우리가 보는 우주의 지평선은 인플레이션이 일어날 당시에는 지평선 거리보다 훨씬 안쪽에 있었으므로 우주의 모습이 닮아 있는 것은 당연한 것이 된다.
우주의 평탄성 문제 역시 인플레이션이론으로 설명된다. 우주의 급격한 팽창은 우주 초기에 있었을지도 모르는 우주의 곡률을 거의 0으로 접근시킨다. 이것은 작은 풍선표면의 곡률은 매우 크게 느껴지지만, 지구표면에서는 지구의 곡률을 느낄 수 없는 것과 같다. 현재 우주가 곡률이 거의 0인 평평한 우주로 인식되는 것은 인플레이션으로 우주가 충분히 크게 팽창하였기 때문이다.